

2024-04-11
曹阳
齐齐哈尔二机床(集团)有限责任公司
普通数控机床一般有X、Y、Z三个直线轴,在给机床各坐标轴命名时,一般都是先命名直线轴中的主轴(Z轴),因为主轴和机床关联很大,是机床重要的组成部件,刀具的装夹、工件的切削、动力与切削力的转换都由主轴实现,可以说主轴是整个数控机床的心脏。主轴定位精度直接决定工件的加工质量和加工精度。
1 加工误差的产生
在数控机床进行机械加工时,造成主轴热变形的热源分为外部热源和内部热源,无论是机床内部摩擦产生热源,还是由于外部环境对数控机床的温度产生影响,根据物理学可知,金属在受热后会发生膨胀。因为机床零件结构、材料的差异性使每个零件温升、变形量(拉伸、扭曲等)都不相同,由于温度的升高使数控机床的主轴产生一定位移,造成加工刀具和加工件之间错位,即造成加工误差,如图1所示。
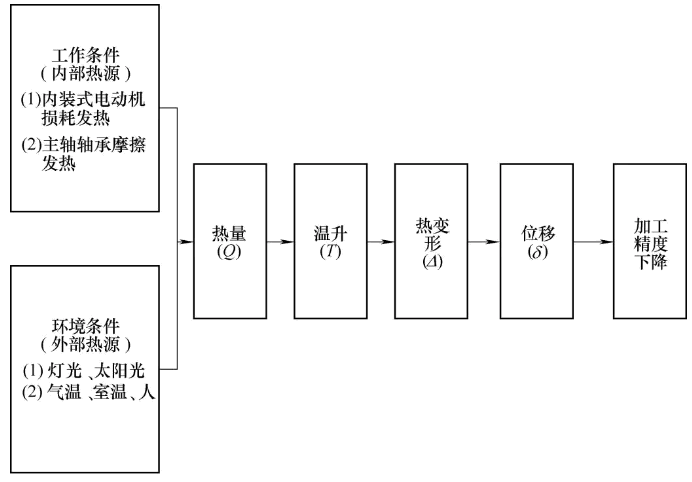
图1 数控机床主轴产生热误差的条件
2 机床热态分析方法
机床受温度影响发生热变形而产生的误差为热误差。在各种类型的误差中,热误差可占机床误差的40%~70%,是影响机床加工精度的主要因素。而机床主轴的热误差直接反映在机床加工零件的质量上。目前,针对热态特性,可以采用以下两种方法对数控机床主轴进行热态分析。
(1)有限元分析法:使用有限元法对滑枕进行热变形分析,建立滑枕模型。对滑枕的外部热源和内部热源等参数进行计算,和滑枕有限元分析后的模型组建热误差模型,仿真分析出滑枕内部温度分布情况,得到滑枕内部的热变形误差。
(2)测量法:该方法是在滑枕内部安装温度传感器,直接测量数控机床主轴在工作时的温度情况,使用激光位移传感器对主轴的热伸长情况进行测量,临末对温度和热变形进行分析。
有限元分析法可深入分析滑枕内部热源及周围环境影响下的热态特性,能对主轴的热变形有简单直观的认识。但对机床的影响因素很多,不能把所有的因素全部参数化,所以通常造成数值仿真结果与实际存在一定程度的偏差,这样影响热误差补偿的精确度。
测量法则可直接测量机床的温度和位移情况,但是由于传感器无法布置到机床各个点,无法得到整个机床的温度和热变形数据,而且试验时间较长。由于每台机床的装配精度、轴承与滑枕的间隙、轴承的发热量以及外界温度等都不可能完全一致,导致每台机床在出厂前都需要进行测量,而且在厂家安装后的环境和在装配现场的环境也存在差异,导致在装配现场的数据不能适用于用户的使用环境,安装后仍需重新进行热误差补偿。有限元分析法和直接测量法在获得数控机床热态特性过程中都存在利与弊,但是这两种方法相辅相成,具有较强的互补性,因此在生产过程中会结合这两种方法使用。
3 落地数控铣镗床主轴温度补偿
数控TK6920落地铣镗床主轴的热误差主要是由于机床进行加工作业时,将会产生很多较复杂的温度场,进而对数控机床整体部件产生影响,并且由于受热原因产生形变。从TK6920落地铣镗床主轴的温度变化情况可以发现主轴受热后的变形规律。
TK6920落地铣镗床滑枕的内部结构相对比较简单,发热源主要为主轴的轴承,其他部件引起的发热太小,可以忽略。主轴上的轴承采用进口的高精度组配轴承,价格昂贵,所以将温度传感器设置在主轴轴承上,这样既检测了主轴的温度,同时也能起到监测轴承温度的作用,一旦轴承出现温度过高、超出安全温度时,系统会自动报警,机床停止运行。
由于不同条件下补偿模型也不同,误差模型不具有通用性,补偿的准确率低,同时结合该机床的特点,本文采用测量法进行补偿。
在铣轴前五个轴承上分别布置五个温度传感器T1、T2、T3、T4和T5。如图2所示,温度传感器T1、T4主轴转速在1 000r/min、环境温度在20℃时运行180min,每15min记录一次前轴承温度值,由于温度传感器T1、T2和T3所对应的轴承尺寸、安装位置、转速、润滑条件及工作环境都相同,并且产生的热位移也基本相同,所以以传感器T1数据代表主轴前轴承温度值。T4、T5所对应的轴承尺寸、安装位置、转速、润滑条件及工作环境都相同,并且产生的热位移也基本相同,所以以传感器T4数据代表主轴后轴承温度值。主轴热位移如图3所示。
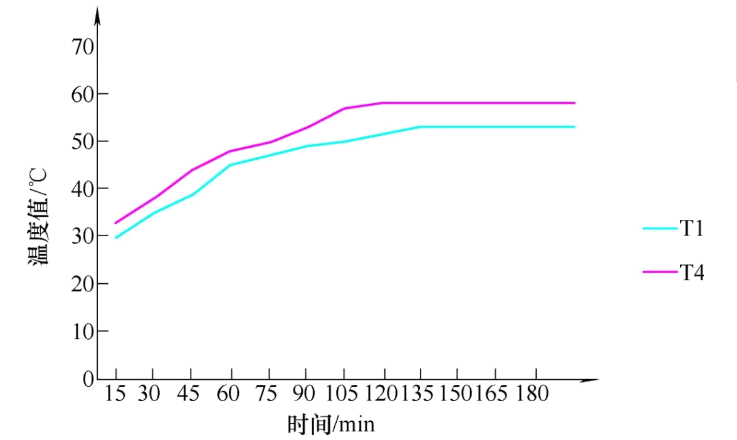
图2 传感器T1热误差变化

图3 主轴热位移
根据试验数据,采用多元回归二乘法建立热误差补偿模型,即Z=5.09+10.18×ΔT1+2.13×ΔT4。
图4所示为数控机床实时补偿示意图,补偿控制器由CNC处理部分、CNC控制部分和传感器部分组成。
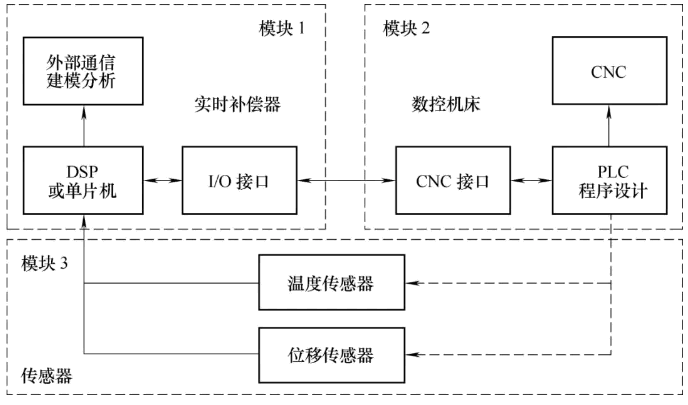
图4 数控机床实时补偿示意图
构建即时监控系统能够有效对热误差进行补偿作业。构建后能够通过测量数据得到即时误差补偿值,其中还要满足以下几个关键要素:首先要利用温度传感器测量主轴和位移传感器测得的数据,用多元回归二乘法进行计算,计算出热变形误差补偿方程。将计算得到的模拟数据转换为数字数据。使用PLC计算出主轴需要的补偿值并传给数控系统,临末通过数控系统实现补偿。
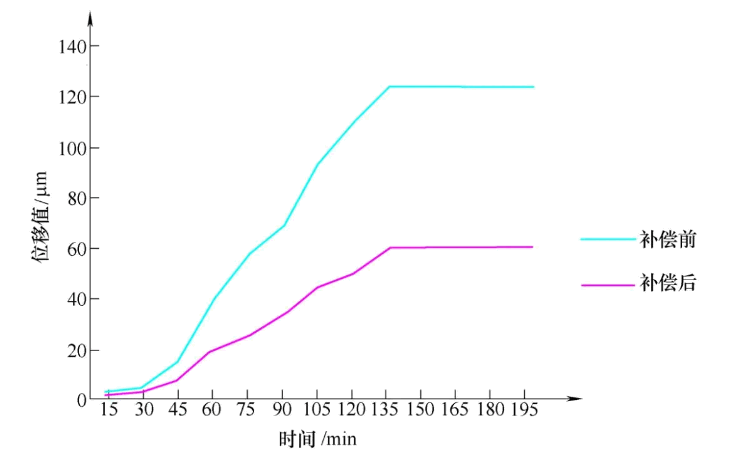
图5 主轴热误差补偿前、后对比
通过图5可以发现,多元回归二乘法可以很好地对主轴的热误差进行补偿。但也有其局限性,主轴在不同的转速下不能用同一数学模型表示,此模型只适合主轴转速在1 000r/min时的热误差补偿。机床运行180min后,主轴的位移值由124μm减小到67μm。
来源:《金属加工(冷加工)》杂志